Расчет годовых процентов

Способ расчета сложного процента

Плата за пользование полученными деньгами (в случае кредита) и вознаграждение за передачу собственных средств на хранение (в случае депозита) в основном вычисляются с помощью второго вида доходности. Расчет годовых процентов сложного типа включает в себя процент, учитывающий как начисление на сумму вклада, так и сумму ранее начисленных по вкладу процентов. При этом периодичность и срок договора также входят в условия расчета капитализированного процента. Ниже представлена формула расчета суммы процентов. Годовые значения имеют наращенный характер. Далее представлено на примере, какой из методов начисления процентов является наиболее выгодным для потребителя.

Формула расчета годовых процентов показывает, что вклад или кредит с капитализацией обязательно должен иметь периодичное начисление процентов. Это приводит к тому, что разбитый на периоды срок банковского договора способствует начислению процента за каждый временной промежуток с последующей капитализацией. Месяц выступает в роли наиболее популярного периода причисления процента, доход которого определяется по календарным дням. Поэтому совокупная прибыльность вклада выводится по сумме процентов, начисленных по отдельным периодам.

Вычисление APY с помощью формулы

Если вы предпочитаете выполнять математические расчеты по старинке, вычислите APY вручную следующим образом:

APY = 100 [(1 + r/n)^n] – 1, где r – заявленная годовая процентная ставка в виде десятичного числа, а n – количество периодов начисления сложных процентов в год. (Карет («^») означает «возведены в степень.»)

Продолжая предыдущий пример, если вы получаете 51,16 доллара США процентов в течение года при балансе счета в 1000 долларов США, рассчитайте APY следующим образом:

• APY = 100 [(1 + .05/12)^12] – 1]
• APY = 5.116%

Вы также можете рассчитать годовую процентную доходность следующим образом:

APY = 100 [(1 + Процент/Основная сумма)^(365/Дни в срок) – 1], где проценты – это сумма полученных процентов, а основная сумма – это начальный депозит или остаток на счете.

Используя выплату процентов и остаток на счете из приведенного выше примера, рассчитайте APY следующим образом:

• APY = 100 [(1 + 51.16/1000)^(365/365) – 1]
• APY = 5.116%

Максимизация APY

Годовая процентная доходность увеличивается с более частыми периодами начисления сложных процентов. Если вы откладываете деньги на банковский счет, узнайте, как часто они накапливаются. Ежедневное или ежеквартальное начисление сложных процентов обычно лучше, чем годовое, но для уверенности проверьте APY для каждого счета.

Вы также можете увеличить APY самостоятельно, если посмотрите на все свои активы как на часть более широкой финансовой картины. Другими словами, не думайте об инвестиции в один депозитный сертификат (ДС) в отдельности от вашего текущего счета – все вложения должны работать вместе, помогая вам достичь ваших целей, и каждое из них должно располагаться соответствующим образом.

Чтобы максимизировать вашу личную годовую процентную доходность, убедитесь, что ваши деньги увеличиваются как можно чаще. Если два ДС дают одинаковую процентную ставку, выберите тот, который выплачивает проценты чаще (и, следовательно, имеет самую высокую процентную ставку). Вы можете автоматически реинвестировать свой процентный доход – чем чаще, тем лучше – и вы начнете получать больше процентов с этих процентных платежей.

Расчёт суммы процентов по кредиту с помощью кредитного калькулятора онлайн

В любом из возможных случаев, мы рекомендуем пользоваться кредитным калькулятором онлайн. Это полностью убирает человеческий фактор, возможность сотрудника банка злоупотребить Вашим доверием и просто облегчает расчёты кредита.

К фиксированным мы относим процентную ставку. Да, некоторые банки предоставляют возможность использования изменяемой кредитной ставки, но об этом мы говорили в другой статье. К не фиксированным процентам мы относим комиссии: “за досрочное погашение кредита”, “за выдачу наличных”, “за просроченный платёж по кредиту” и другие. Воспользуйтесь блоком досрочное погашение, если Вы уже совершали его. Добавьте ежемесячные и единоразовые комиссии, это позволит рассчитать всю сумму процентов по кредиту.

Нажмите кнопку “Рассчитать” и Вы получите полный график платежей, включая процентную ставку, указанные ранее комиссии и досрочные погашения кредита

Обратите внимание на блок “Общие данные”, в нём есть колонка “Начисленные проценты” – это и будет сумма процентов по кредиту. Если Вы хотите более детально рассмотреть в какой из месяцев и сколько заплатите процентов по кредиту, нажмите на кнопку “Загрузить ещё … количество строк”

Распечатайте на принтере, сохраните или отправьте по электронной почте график платежей. Это позволит сравнить полученный график с графиком представленным банком. Так Вы легко поймете о скрытых комиссиях и возможных переплатах, о которых банк умолчал ранее.

Пример будущей стоимости денег

Задача № 3

Найти будущую стоимость (БС) актива, если планируется вложение 5000 рублей, под 10,5 % годовых на 3 года.

В этой задаче текущей стоимостью (ТС) будет являться 5000 рублей, а БС этих же средств рассчитывается двумя способами. Первый без реинвестирования, а второй с учетом реинвестирования данных средств. Тогда данные расчеты выступают аналогом простых и сложных процентов.

Формула использования сложных процентов выглядит следующим образом:

Где:

• FV (англ. Future Value) — будущая стоимость денег.
• PV (англ. Present Value) — текущая или первоначальная стоимость.

Использование простых процентов выглядит так же, но записанная в скобки ставка процентов не возводится в степень, а умножается непосредственно на количество периодов.

Тогда в задаче, представленной выше, БС с применением простых процентов будет равна:

FV = 5000 х (1 + 5 х (10,5 : 100)) = 5000 х 1,525 = 7625.

А с применением сложных процентов иначе:

FV = 5000 х (1 + (10,5 : 100))^5 = 5000 х 1,647 = 8235.

Разница в доходности составит 610 рублей. Отсюда, взаимодействовать с финансовыми организациями, использующими сложные проценты для своих расчетов, намного выгоднее.

Чтобы сравнить денежные притоки по инвестициям, которые осуществляются в разные сроки, нужно привести их к одному моменту времени. Эта процедура называется дисконтированием, если финансовые поступления приводятся к начальному периоду, и наращением, если к будущему моменту времени. Однако в обоих случаях формула расчета процентов не изменяется. Меняется только расположение процентного множителя.

Эффективная процентная ставка по вкладу

Эта характеристика актуальна только для вкладов с капитализацией процентов. В связи с тем, что проценты не выплачиваются а идут на увеличение суммы вклада, очевидно, что если ежемесячно возрастает сумма вклада, то и вновь начисленные на эту сумму проценты также будут выше, как и конечный доход.

Если рассчитать, сколько процентов было начислено к начальной сумме к концу срока вклада, эта величина и будет являться эффективной процентной ставкой.

Формула расчета эффективной ставки:

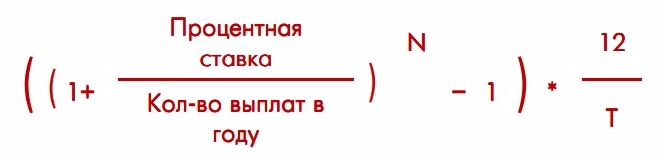
где

• N – количество выплат процентов в течение срока вклада,
• T – срок размещения вклада в месяцах.

Эта формула не универсальна. Она подходит только для вкладов с капитализацией 1 раз в месяц, период которых содержит целое количество месяцев. Для других вкладов (например вклад на 100 дней) эта формула работать не будет.

Однако есть и универсальная формула для расчёта эффективной ставки. Минус этой формулы в том, что получить результат можно только после расчёта процентов по вкладу.

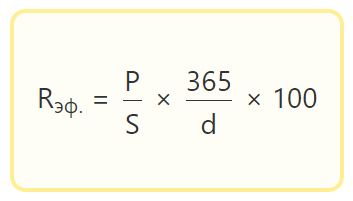
• R_эф. – эффективная ставка
• P – проценты, начисленные за весь период вклада
• S – сумма вклада
• d – срок вклада в днях

Эта формула подходит для всех вкладов, с любыми сроками и любой периодичностью капитализации. Она просто считает отношение полученного дохода к начальной сумме вклада, приводя эту величину к годовым процентам. Лишь небольшая погрешность может присутствовать здесь, если период вклада или его часть выпала на високосный год.

Именно этот метод используется для расчёта эффективной ставки в представленном здесь депозитном калькуляторе.

Как рассчитать проценты по вкладу онлайн?

Если вы боитесь допустить ошибку в расчете или не обладаете специальными знаниями, то можно пойти по простому пути. Многие крупные банки позаботились о своих клиентах и разработали онлайн-калькулятор. Рассмотрим, как сделать расчет на примере Сбербанка.

В открывшемся окне будет вся информация по вкладу. Ваша задача – немного пролистать страницу и найти калькулятор. В калькуляторе можно выбрать/указать:

• сумму;
• срок;
• способ оформления: онлайн или через офис (при выборе второго варианта снять галочку);
• статус клиента: пенсионер или нет;
• с капитализацией или нет.

Моментально справа рассчитается доход по вкладу, с учетом процентной ставки по договору.

Стоит отметить преимущества СБЕРа, которое есть не у всех. Банк предлагает посмотреть формулу, по которой делается расчет.

Основные правила начисления вознаграждения

Финансовые вычисления включают в себя также анализ инвестиционного процесса. Ведь годовые проценты применяются не только для расчета традиционных методов сохранения средств, то есть для сберегательных вкладов, но и для оценки инвестиций на фондовом рынке. Ниже представлены основные принципы расчета, относящиеся ко всем типам приумножения капитала.

Если процент – это денежные поступления в качестве дохода, то простой и сложный процент – это ставки, по которым этот доход начисляется с определенной периодичностью на тело вклада или долга. При рассмотрении двух видов процента можно заметить, как индивид получает большую доходность, если банк используется сложные проценты. Это связано с постоянным реинвестированием накопленного дохода.

Сложный процент. Формулы расчета сложного процента

Люди во все времена думали о своем завтрашнем дне. Они старались и стараются обезопасить от финансовых невзгод и себя, и своих детей и внуков, строя хотя бы небольшой островок уверенности в будущем. Начиная строить его уже сейчас с помощью небольших банковских вкладов, можно обеспечить себе в дальнейшем стабильность и независимость.

Основным принципом банковских операций является то, что денежные средства способны увеличиваться лишь тогда, когда находятся в постоянном обороте. Чтобы клиентам уверенно ориентироваться в сфере финансовых услуг и уметь правильно подбирать условия, выгодные им в определенный промежуток времени, необходимо знать ряд простых правил. В данной статье речь пойдет о долгосрочных вложениях, которые позволяют за определенное количество лет из относительно небольшой суммы начального капитала получить существенную прибыль или использовать вклад дальше, снимая начисления для повседневных нужд.

Для правильного расчета прибыли необходимо выполнить несложные арифметические действия на основе нижеизложенных формул.

Формула сложного процента (расчет в годах)

Например, вы решили положить 100000,00 руб. под 11% годовых, чтобы через 10 лет воспользоваться сбережениями, которые значительно выросли в результате капитализации. Для расчета итоговой суммы следует применить методику расчета сложного процента.

Применение сложного процента подразумевает то, что в конце каждого периода (год, квартал, месяц) начисленная прибыль суммируется с вкладом. Полученная сумма является базисом для последующего увеличения прибыли.

Для расчета сложного процента применяем простую формулу:

где

• S – общая сумма («тело» вклада + проценты), причитающаяся к возврату вкладчику по истечении срока действия вклада;
• Р – первоначальная величина вклада;
• n — общее количество операций по капитализации процентов за весь срок привлечения денежных средств (в данном случае оно соответствует количеству лет);
• I – годовая процентная ставка.

Подставив значения в эту формулу, мы видим, что:

через 5 лет сумма будет равняться 168505,81 рублей:

а через 10 лет она составит  283942,09 рублей :

Если бы мы рассчитывали капитализацию процентов по вкладу за короткий период, то сложный процент было бы удобнее рассчитывать по формуле

где:

• К – количество дней в текущем году,
• J – количество дней в периоде, по итогам которого банком производится капитализация начисленных процентов (остальные обозначения – как и в предыдущей формуле).

Но тем, кому удобнее ежемесячно снимать проценты по вкладу, лучше ознакомиться с понятием «капитализация вклада», подразумевающим начисление простых процентов.

На графике показано как вырастет капитал при капитализации процентов по вкладу, если вложить 100000,00 руб. на 10 лет под 10%, 15% и 20%

Формула сложного процента (расчет в месяцах)

Существует и другой, более выгодный для клиента метод начисления и прибавления процентной ставки – ежемесячный. Для этого применяется следующая формула:

где n также соответствует количеству операций по капитализации, но уже выражается в месяцах. Процентный показатель здесь дополнительно делится на 12 потому что в году 12 месяцев, а у нас появляется необходимость в расчете месячную процентную ставку.

Если бы данная формула использовалась для поквартального начисления вклада, то годовой процент делился бы на 4, а показатель n был бы равен количеству кварталов, а если бы процент начислялся по полугодиям, то процентная ставка делилась бы 2, а обозначение n соответствовало количеству полугодий.

Итак, если бы нами был сделан вклад в сумме 100000,00 руб. с ежемесячной капитализацией процентов, то:

через 5 лет (60 месяцев) сумма вклада выросла бы до 172891,57 руб., что примерно на 10000 руб. больше, чем в случае с ежегодной капитализацией вклада;руб.

а через 10 лет (120 месяцев) «наращенная» сумма составила бы 298914,96 руб., что уже на целых 15000 руб. превосходит показатель, рассчитанный по формуле сложного процента, предусматривающей расчет в годах.

Это означает, что доходность при ежемесячном начислении процентов оказывается больше, чем при начислении один раз в год. И если прибыль не снимать, то сложный процент работает на пользу вкладчика.

График, показывающий разницу роста капитала при расчете в годах и при ежемесячной капитализации процентов

По данным с http://101.credit/articles/vkladi/clozhnyjj-procent/

Как вычислить проценты за оплату

Пока длится льготный период, держателю карты несколько раз поступит смс-уведомление о необходимости внесения минимального платежа. Он составляет 5% от суммы задолженности, но не менее 300 рублей, и идёт в счёт погашения долга.

Этот платёж — аналог ежемесячных взносов по обычному кредиту. Отличие в том, что его величина постоянно меняется. Рекомендуется вносить большую сумму, чем указано в банковском уведомлении.

Когда льготный период окончен, в сумму оплаты включаются проценты по кредиту.

Предположим, сумма долга на дату расчёта платежа составляет 10 000 рублей. Ставка — 23,99% годовых. Тогда банк выставит к оплате:

• •

  5% от 10 000 рублей – 500 рублей. Эта сумма идёт на погашение основного долга.

• •

  При ставке 23,99% годовых в день на эту сумму начисляется 6,57 рублей, а за месяц — 197,10 рублей.
  Итого минимально нужно внести 697,10 рублей.

За просрочку минимального платежа предусмотрен штраф. Он указан в условиях кредитования и составляет 20% годовых от суммы взноса, т.е. 0,055% в день (для договоров, заключённых ранее, размер может варьироваться). Штраф применяется, если платёж:

• •

  Не внесён совсем;

• •

  Внесён в меньшем объёме, чем нужно;

• •

  Внесён после указанного в сообщении срока.

Например, долг составляет 50 000 рублей. Значит, размер минимального платежа – 2 500 рублей. Если протянуть с оплатой, придётся дополнительно вносить 1,375 рублей за каждый день просрочки (2 500 * 0,055% = 1,375).

Виды процентных ставок по вкладам в банках

Открывая депозит в банке, у вас есть возможность решить, что вы хотите делать с начисляемыми дивидендами – выводить их на карту или прибавлять к сумме первоначального вклада, тем самым капитализируя его. В зависимости от того, какой вариант вы выберете, такой будет и формула расчета процентов. Если вы хорошо помните школьную математику, то вы знаете, что проценты бывают простыми, а бывают сложными.

Как начисляются простые проценты?

Итак, простая ставка по депозитам рассчитывается следующим образом:

Для удобства понимания давайте разберем такой пример: вы открываете в банке депозит на сумму в 50 000 рублей на 1 год с простым начислением процентов. Ставка % составляет 11,5%. Пользуясь вышеуказанной формулой, получается, что через год, после того как будет закрыт ваш депозит, вы заработаете:

В данном случае проценты не будут прибавляться к телу депозита, а каждый месяц (раз в полгода или раз в год) будут выводиться на другой ваш счет. Очень выгодно в таком случае пользоваться ежемесячным выводом процентов на дебетовые карты с начислением процентов на остаток. Если вы не успеваете потратить заработанные на депозите средства, на них будет начислен % по вашей карте.

Как начисляются сложные проценты?

Расчет сложных процентов по вкладу несколько сложнее и интереснее. Однако, прежде, чем мы приступим к его изучению, я предлагаю вам выяснить, в каких случаях мы имеем дело со сложной ставкой.

Открывая в банке депозит, вы вправе решать, прибавлять к нему полученные проценты или выводить их на другой счет. В случае, если вы выбираете первый вариант, по вашему вкладу начисляется сложный процент. То есть, в каждом последующем периоде % начисляются на большую сумму, нежели в предыдущем, тем самым ускоряя рост размера депозита.

Это присоединение выплат по депозиту к первоначальной сумме вклада очень важно, поскольку сумма накоплений растет все быстрее и быстрее. Причем, моделью роста выступает не арифметическая прогрессия, а экспонента

Для сравнения давайте возьмем расчет простых и сложных процентов по одному и тому же вкладу. Условно положим на счёт 100 000 рублей под 10% годовых. В конце расчетного периода по простой ставке мы получим:

100 000 * 10 / 100 = 10 000 рублей;

Чтобы посчитать доходность вкладов с капитализацией выведем общую формулу:

Формула сложных процентов представлена ниже:

Переменные означают следующее,

Рассчитываем наш пример:

100 000 * (1+0,833*365 / 100*365)^12 = 10 466,92 рублей

Таким образом, один и тот же депозит, положенный в банк на разных условиях, может принести как 10 000 рублей чистой прибыли, так и 10 466 рублей.

В последнем случае мы имеем дело с капитализацией депозита – добавлением начисленных % к телу депозита. Как результат, получаем рост первоначальной суммы инвестиции и начисление % на увеличенную сумму.

Чтобы не считать доходность депозита вручную, советую вам воспользоваться калькулятором сложных процентов. В нем вы сможете указать суммы регулярных довложений за определенный период. Найти такой калькулятор можно на моем сайте с правой стороны, в сайдбаре, во вкладке «Калькулятор доходности».

Как начисляется эффективная ставка?

Ну а теперь давайте разберемся с эффективной процентной ставкой по депозиту, чтобы собрать в голове полную картинку банковских предложений.

Эффективной ставкой принято называть ставку, дающую равнозначный доход по идентичному депозиту без капитализации процентов. То есть, предположим, что вы открываете счёт в размере 50 000 на год под 8% годовых с условием капитализации. Проводим расчет по уже известной нам формуле и получаем:

50 000 * (1+0,6666*365/100*365) 12 = 54 150 рублей.

А теперь смотрим на предложение в соседнем банке. Здесь вы можете открыть тот же самый депозит, но без капитализации, зато под 8,3% годовых. Такое предложение позволит вам получить точно такой же доход, как в случае с капитализацией.

(50 000 * 8,3 * 365/365) / 100 = 4 150 рублей.

Чтобы быстро рассчитать эффективную ставку по депозиту, достаточно сделать следующее:

Именно эти 8,3% и являются нашей эффективной годовой ставкой по депозиту с ежемесячной капитализацией. То есть, если вклад без прибавления процентов к телу депозита будет иметь ставку, превышающую 8,3%, то такое вложение будет для нас более выгодно, нежели депозит с 8% годовых и ежемесячной капитализацией. Не забываем, что в случае с вкладом с 8.3% годовых, ежемесячный процент можно перевести на дебетовую карту с начислением на остаток, в этом случае этот вклад будет выгоднее.

Пример второй – Капитализация процентов ежеквартально

Капитализация процентов ежеквартально

Капитализация процентов – ежеквартально. Применяем формулу сложных процентов. Действуем по аналогии с первым примером

Но, обращаю ваше внимание на достаточно распространенную ошибку при расчете. Многие, при расчете ежеквартальной капитализации, подставляют в формулу j – неправильное количество дней

Нужно ставить не 30 или 31 день, по количеству дней в месяце, а количество дней за общий календарный период. Для этого мы суммируем количество дней за 3 месяца каждого квартала.

• В первом квартале – это будет 90, либо 91 день, в зависимости от того, сколько дней в феврале, например: Январь (31 день) + Февраль (28 дней) + Март (31 день) = 90 дней.
• Во втором квартале – это будет 91 день: Апрель (30 дней) + Май (31 день) + Июнь (30 дней) = 91 день.
• Во третьем квартале – это будет 92 дня: Июль (31 день) + Август (31 день) + Сентябрь (30 дней) = 92 дня.
• Во четвертом квартале – это будет 92 дня: Октябрь (31 день) + Ноябрь (30 дней) + Декабрь (31 день) = 92 дня.

1 кв.: S=(100 000 х 14 х 90 / 365) / 100S=3452,05 руб. Прибавляем это к первоначальной сумме. Получаем 103452,05 руб. Дальше по аналогии с первым примером.

Пример первый – Капитализация процентов ежемесячно

Капитализация процентов ежемесячно

В этом случае, мы применяем формулу сложных процентов, так как капитализация процентов происходит ежемесячно.

Янв: S=(100 000 х 14 х 31 / 365) / 100S=1189,04 руб.

Далее, получившийся процент в размере 1189,04 руб., мы прибавляем к нашему первоначальному вкладу в размере 100.000 руб. Получаем 101 189,04 руб. Так выглядит ежемесячная капитализация. Дальше февраль рассчитываем аналогичным образом, не забывая про то, что в феврале 28 или 29 дней.

Фев: S=(101 189.04 х 14 х 28 / 365) / 100S=1086,74 руб. (сумма получилась меньше, так как в феврале было меньше дней, чем в предыдущем месяце). Прибавляем полученные проценты 1086.74 к 101189,04 = 102275,78 руб. И так далее, полученные проценты прибавляем к предыдущей сумме и расчет нового месяца делаем с учетом первоначального вклада и всех накопленных процентов.

Формулы простых и сложных процентов

Поскольку простые и сложные проценты чаще всего используются при расчете прибыли от банковских вкладов, продолжим на их примере. Для решения задач нам понадобится такая информация:

• К — начальная сумма вклада;
• К — конечная сумма вклада;
• R — ставка доходности, переводится из процентов в число (10% = 0.1);
• N — количество периодов (лет).

Формула простого процента

По этой формуле мы можем рассчитать конечную сумму вклада без капитализации полученной прибыли. Для этого нужно знать начальную сумму вклада, процентную ставку за 1 период инвестирования и временной интервал. Если конечная сумма задана сразу и нужно найти другую неизвестную переменную, используйте производные формулы простого процента:

Формула сложного процента

По этой формуле мы можем посчитать конечную сумму вклада с учётом капитализации полученной прибыли, зная начальный депозит, процентную ставку и нужный временной интервал. Для решения задач также можно использовать производные формулы сложного процента:

На практике часто дело не заканчивается первоначальным депозитом — многие пользуются регулярными пополнениями, например делают регулярные инвестиции из зарплаты. Для этих случаев формула сложного процента становится длиннее:

где D — сумма регулярных пополнений банковского депозита

Обратите внимание, степень N-1 означает, что доливки начинаются со второго инвестиционного периода (если сумма дополнительных инвестиций вносится сразу, то N-1 меняется на N)

Ну что, удачи на экзаменах всем читающим меня студентам 🙂 Для закрепления далее мы разберем несколько примеров задач на сложные проценты.

Примеры подсчетов по депозитам

Чтобы показательно привести расчет процентовки по простым и сложным депозитам, стоит применить уже указанные формулы. За пример возьмем открытие депозита стоимостью в 500 000 руб. длительностью в год по банковской ставке в 12%.

Простой депозит. Подставляем наши цифры в существующую формулу: (500 000 х 12 х 365 / 365) х 100. Получаем итог в 60 000 руб. То есть доходность вкладчика составит 60 000 за год.

Сложный вклад. Будем исходить из тех же цифр с учетом открытия вклада на период в 3 месяца. Подставляем их в имеющуюся формулу:

1. Доход за первый месяц: (500 000 х 12 х 3 / 365) х 100 = 4 930 руб.
2. Доход за второй месяц: ((500 000 + 4 930) х 12 х 3 / 365) х 100 = 4 980 руб.
3. Доход за третий месяц: ((500 000 + 4 930 + 4 980) х 12 х 3 / 365) х 100 = 5 029 руб.

Из полученных данных можно понять, что наиболее выгодными являются вклады сложные, открытые с условием капитализации процентовки. И эта выгода очевидна при рассмотрении депозитов, оформленных на одинаковые суммы с одной процентной ставкой. Это нужно учитывать потенциальным вкладчикам.

Основные правила начисления процентов

Подведём краткий итог:

• •

  Во время льготного периода плата не начисляется.

• •

  По окончании грейс-периода проценты начисляются за каждый день пользования деньгами банка.

• •

  Начисление происходит не на весь предоставленный лимит, а только на сумму задолженности.

• •

  После полного погашения долга проценты перестают начисляться, и вы можете снова воспользоваться льготным периодом.

• •

  Если вы не вносите никакие средства во время льготного периода, его действие прекращается досрочно.

• •

  Банк удерживает неустойки и штрафы за нарушение сроков возврата средств.

Если вы боитесь не уложиться с возвращением долга в срок, выбирайте карту со льготным периодом 100 дней. Она даст вам дополнительный запас времени.

Расчет кредита на онлайн-калькуляторе

Сегодня кредитные онлайн-калькуляторы размещаются не только на сайтах банков, но и на большинстве специализированных интернет-ресурсов, посвященных финансовой тематике. Причина такой ситуации очевидна и заключается в удобстве и простоте пользования подобными инструментами.

Буквально в течение нескольких секунд любой желающий может рассчитать на кредитном калькуляторе онлайн примерные параметры доступного кредита. Примеры подобных расчетов приведены в таблице.

Исходные условия кредита	Результат расчета
Сумма	Срок	Ставка	Ежемесячный платеж, руб.	Величина переплаты, тыс. руб.	Общая сумма выплат, млн. руб.
450 тыс. руб.	Полгода	12%	77 647	15,785	0,466
500 тыс. руб.	Год	12%	44 424	32,978	0,533
1 млн. руб.	Год	18%	91 680	99,798	1,100
1,5 млн. руб.	2 года	15%	72 730	245,144	1,745
2 млн. руб.	Год	11%	176 763	120,744	2,121
3 млн. руб.	5 лет	11%	65 227	912,792	3,913
5 млн. руб.	5 лет	10%	106 235	1 372,894	6,373
5 млн. руб.	7 лет	10%	83 006	1 971,075	6,971

Возможность предварительно рассчитать кредит позволяет определить наиболее важные его параметры, к числу которых относятся: величина регулярной выплаты, сумма переплаты и общий размер платежей по займу в целом. Сравнение нескольких вариантов расчетов наглядно показывает, какой вариант кредитования наличными наиболее выгоден для потенциального заемщика.

Расчет процентов по кредиту

Ключевым параметром для сравнения различных кредитов выступает величина выплаченных процентов или, как часто называют этот показатель, сумма переплаты. Именно она, наряду с эффективной процентной ставкой, демонстрирует реальную выгодность того или иного банковского продукта для клиента. Ниже приводятся примеры расчетов разных кредитов, отсортированные по данному параметру.

Исходные условия кредита	Результат расчета
Сумма	Срок	Ставка	Размер переплаты	Ежемесячный платеж	Общая сумма выплат, млн. руб.
500 тыс. руб.	Год	10%	27 402 руб.	43 958 руб.	0,527
500 тыс. руб.	1,5 года	10%	40 433 руб.	30 029 руб.	0,540
750 тыс. руб.	Год	10%	41 102 руб.	65 937 руб.	0,791
1 млн. руб.	Год	10%	54 803 руб.	87 916 руб.	1,055
750 тыс. руб.	1,5 года	10%	60 650 руб.	45 043 руб.	0,811
1 млн. руб.	1,5 год	10%	80 866 руб.	60 057 руб.	1,081 млн. руб.

Расчет ежемесячного платежа по кредиту

Не менее серьезное значение в процессе выбора кредита выступает величина ежемесячной выплаты по нему. От величины этого параметра зависит, насколько серьезная финансовая нагрузка ляжет на заемщика. Ниже размещены примеры расчетов условий кредита наличными с выделением данного показателя

Исходные условия кредита	Результат расчета
Сумма	Срок	Ставка	Ежемесячный платеж	Величина переплаты	Общая сумма выплат, млн. руб.
500 тыс. руб.	2 года	10%	23 072 руб.	53 664 руб.	0,554
50 тыс. руб.	Год	12%	44 424 руб.	32 978 руб.	0,533
1 млн. руб.	2 года	10%	46 145 руб.	107 328 руб.	1,107
1 млн. руб.	Год	12%	88 849 руб.	65 957 руб.	1,066
3 млн. руб.	2 года	9,5%	137 743 руб.	305 420 руб.	3,305
5 млн. руб.	3 года	9,5%	160 165 руб.	765 069 руб.	5,795

Формула расчёта процентов по кредитной карте

Если льготный период кончился, а задолженность на кредитной карте осталась, держатель начинает выплачивать банку проценты за весь срок пользования его деньгами, с первого дня образования долга.

Это означает, что размер ежемесячной оплаты будет увеличен. Теперь он состоит не только из основного долга по карте, но и из суммы начисленных за отрезок времени процентов.

Банковская система рассчитывает всё автоматически. В кредитной карте, в отличие от кредита, размер долга — переменная величина, и невозможно предсказать его заранее. Поэтому сумма ежемесячного платежа становится известна только в расчётный день, который наступает каждый месяц в день заключения договора с банком о предоставлении кредитной линии. Далее у вас есть 20 дней на то, чтобы зачислить средства на счёт.

Начисление платы зависит от суммы долга, процентной ставки и количества дней, в которые имелся долг перед банком. Сейчас разберёмся, как это происходит.

Есть два ошибочных убеждения:

1. Что расчёт производится от общей суммы предоставленной кредитной линии. Проценты начисляются исключительно на те средства, которые вы потратили. Чем больше минус счёта, тем больше в итоге окажется размер переплаты.

2. Что проценты начисляются только за дни после завершения льготного срока. На самом деле, если грейс-период завершён, можно считать, что его не было вообще. Если беспроцентный срок по банковской карте 100 дней, и вы внесли долг на 101-й, выплата будет начислена за 101 день.

Чтобы самостоятельно посчитать размер начисленных процентов, нужно:

Что это за программа?

Кредитный калькулятор онлайн — это специальная программа, которая осуществляет предварительный расчет ежемесячного платежа по формуле аннуитетных платежей (то есть равных сумм оплаты в течение всего срока договора), исходя из условий, заданных пользователем.

Платежи рассчитываются в режиме онлайн, то есть результат расчета выдается незамедлительно. Для получения результата не требуется предоставление персональных данных или предварительная регистрация в системе.

В итоговом результате отражаются:

• условия кредитования, заданные пользователем;
• сумма ежемесячного аннуитетного платежа;
• сумма процентов, которые будут уплачены банку за весь срок кредита (переплата);
• график оплат на весь период действия договора (отдельно проценты и кредит);
• список банков, предлагающих услуги кредитования, соответствующих заданным или близких к ним.

Примеры задач

Как рассчитать стоимость кредита

Если вы хотите приблизительно знать, во сколько вам обойдётся банковский кредит, который вы берёте, вот вам простая формула:

полная стоимость кредита=сумма кредита×

Эта формула, как вы понимаете, не учитывает комиссий, платы за обслуживание кредита, страховых взносов, штрафов за просрочку, пени и прочих расходов. Но вы всё равно можете ею пользоваться, чтобы грубо оценить полную стоимость вашего кредита.

Задача. Вы хотите взять 10 млн рублей в ипотеку под 10 % годовых на срок 15 лет (допустим, первый взнос вы уже внесли). Во сколько вам обойдётся данный кредит?

Решение. Полная стоимость кредита составит 10 млн × (1+0,01×10×15)=10 млн × 2,5=25 млн рублей, то есть вам придётся заплатить общую сумму в 25 млн рублей, в которую, помимо суммы долга в 10 млн рублей, входит сумма процентов за пользование кредитом, равная 25–10=15 млн рублей, или 1 млн рублей в год.

Как рассчитать сумму комиссии

Часто нам приходится оплачивать мобильную связь, пополнять электронные кошельки, совершать те или иные платежи. Во всех случаях присутствует тот или иной процент комиссий за пользование сервисом. Как быть, если вы хотите точно знать, какая сумма ляжет вам на счёт или на баланс, или же спишется с вашего электронного кошелька в результате комиссий? Ответ прост. Используйте калькулятор или ваш ум, а также приведённую выше инструкцию вместе со следующей формулой:

сумма с учётом комиссии=требуемая сумма× + фиксированная комиссия

Задача. Какая сумма спишется с баланса мобильного при пополнении с него электронного кошелька, если вы хотите положить на кошелёк 100 рублей, причём комиссионный процент равен 8 %, а фиксированная комиссия составляет 10 рублей?

Решение. Сумма с учётом комиссии будет равна 100×(1+0,01×8)+10=100×1,08+10=118 рублей. Именно такую сумму нужно указать в платежной форме, чтобы у вас на кошельке появились 100 рублей.

Рентабельность вашего бизнеса

Как рассчитать эффективность вашего бизнеса? Для этого нужно знать обобщённые показатели деятельности фирмы, которой вы руководите, такие, как валовая прибыль за прошедший период (который может составлять месяц, квартал, полугодие, год) и общие затраты за тот же период. Тогда вы сможете найти рентабельность вашей деятельности, которая показывает чистую прибыль на 1 рубль затрат:

рентабельность=[(валовая прибыль – общие затраты)/общие затраты]×100 %

Задача. Валовая прибыль вашего бизнеса за прошедший год составила 10 млн рублей при общих затратах в 8 млн рублей. Чему равна рентабельность бизнеса за прошедший год?

Решение. Рентабельность бизнеса равна [(10 млн – 8 млн)/8 млн]×100 %=0,25×100 %=25 %, т. е. на каждый вложенный рубль вы получили доход в 25 копеек.

На сколько % перевыполнен план

Если нужно узнать, насколько величина А больше величины В в процентном отношении, то пригодится следующая формула:

увеличение (прирост) А по сравнению с В=[(А – В)/В]×100 %

Задача. Завод запланировал в текущем квартале выпуск 300 тыс. подшипников, но фактически было произведено 420 тыс. подшипников. На сколько процентов был перевыполнен план по выпуску изделий?

Решение. План за квартал был перевыполнен на [(420 тыс. – 300 тыс.)/300 тыс.]×100 %=

=0,4×100 %=40 %.

На сколько % упала прибыль

Когда вы хотите знать, на сколько величина А меньше величины В в процентном отношении, воспользуйтесь следующей формулой:

уменьшение А по сравнению с В=[(В – А)/В]×100 %

Задача. Прибыль вашего предприятия за последний месяц снизилась со 100 тыс. рублей до 90 тыс. рублей. На сколько процентов упала прибыль за прошедший месяц?

Решение. Снижение прибыли составило [(100 тыс. – 90 тыс.)/100 тыс.]×100 %=10 %.